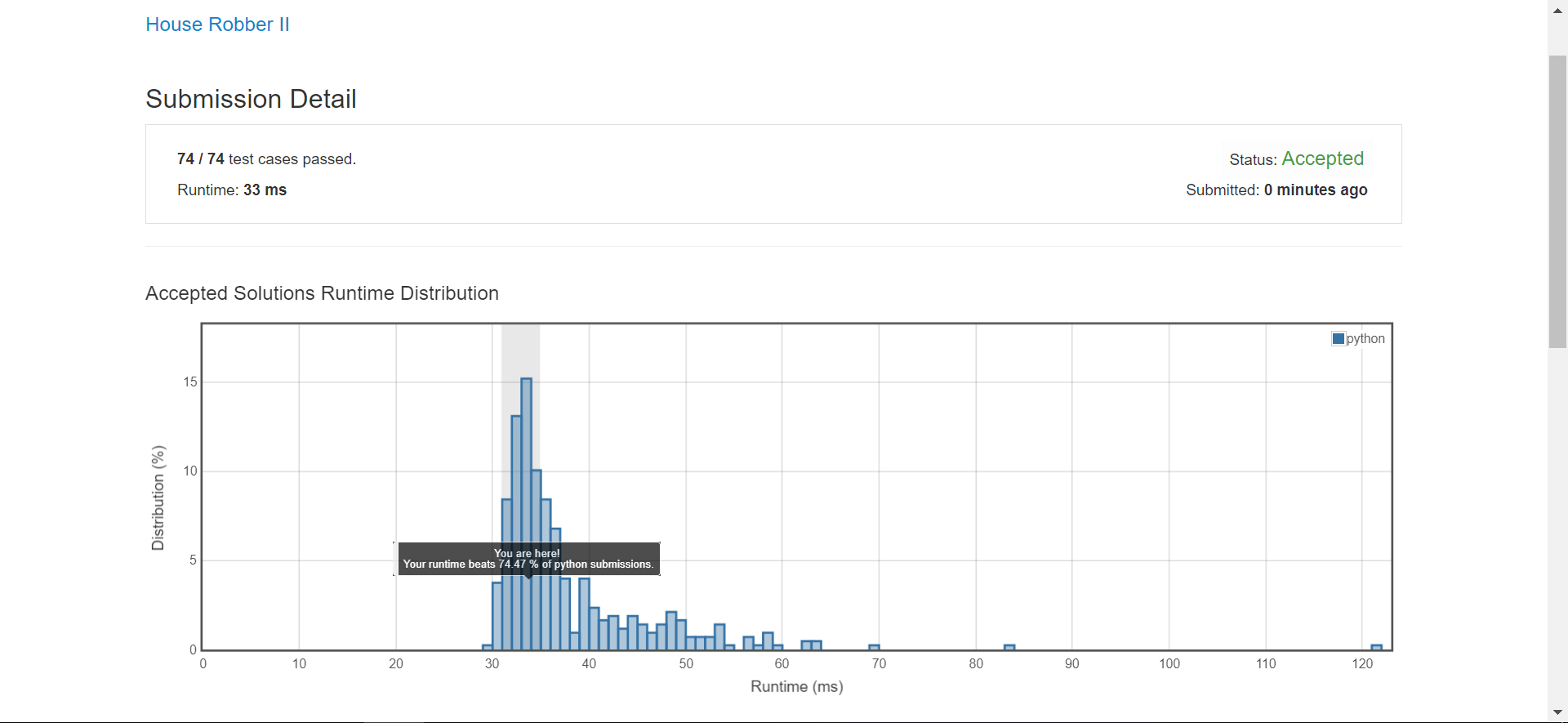
213 House Robber II
原题
After robbing those houses on that street, the thief has found himself a new place for his thievery so that he will not get too much attention. This time, all houses at this place are arranged in a circle. That means the first house is the neighbor of the last one. Meanwhile, the security system for these houses remain the same as for those in the previous street.
Given a list of non-negative integers representing the amount of money of each house, determine the maximum amount of money you can rob tonight without alerting the police.
题意分析
给出一个循环数列(即第一个数与最后一个数相邻),不允许取相邻的数字,求取出数字和的最大值。
题目思路
用动态规划。首先由于是循环数列,因此第一个与最后一个不能同时取到(但可以同时不取到),因此我们分别删除第一个和最后一个进行计算,消除循环队列的影响。由于不能取到两个相邻的数字,因此可以得到状态转移方程:
F(k) = max(F(k-2)+num[k], F(k-1))
补充边界:
F(0) = num[0]
F(1) = max(num[0], num(1))
注意,上述的num数列已经是剔除第一或最后一个数字的数列。
代码(python)
1 | class Solution(object): |
结果
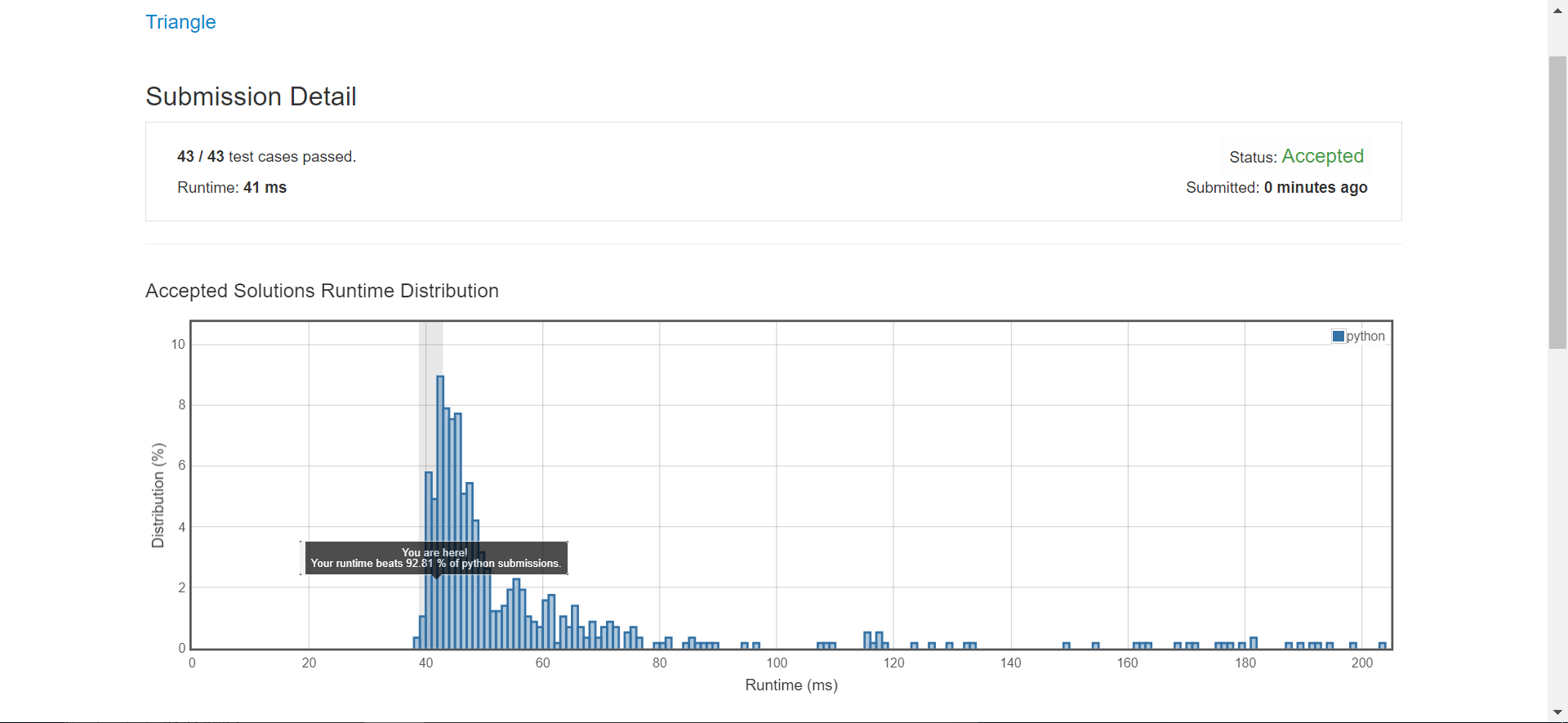
120 Triangle
原题
Given a triangle, find the minimum path sum from top to bottom. Each step you may move to adjacent numbers on the row below.
For example, given the following triangle1
2
3
4
5
6[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]
The minimum path sum from top to bottom is 11 (i.e., 2 + 3 + 5 + 1 = 11).
Note: Bonus point if you are able to do this using only O(n) extra space, where n is the total number of rows in the triangle.
题意分析
在给出的数字三角形中,从顶向下找出一条数字和最小的路径,计算其最小数字和。
题目思路
动态规划,维护一个列表储存上一层(较长的一层,在本题中是下一层)选择各个节点的结果,给出下列状态转移方程(i为行,j为列):
F(0,j) = list(0,j)
F(i,j) = max(F(i-1, j)+list(i,j), F(i-1, j+1)+list(i,j))
由于仅需要上一层第j个和第j+1的信息,因此可以维持一个一维列表即可满足——每次从左至右更新放至列表的第j位。
代码(python)
1 | class Solution(object): |
结果