星球的公转与自转

Posted on | In | | Visitors:

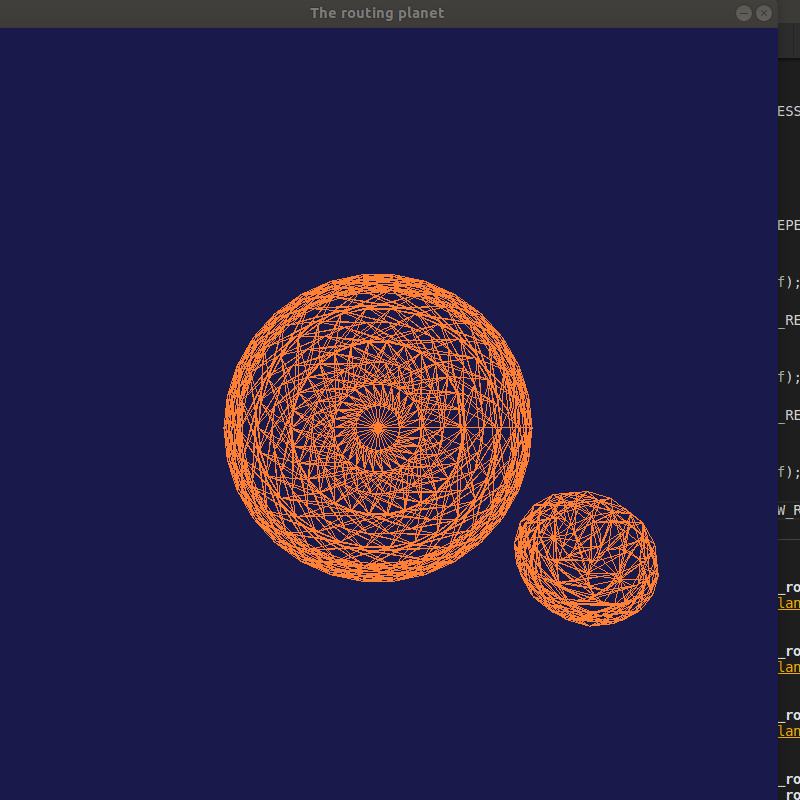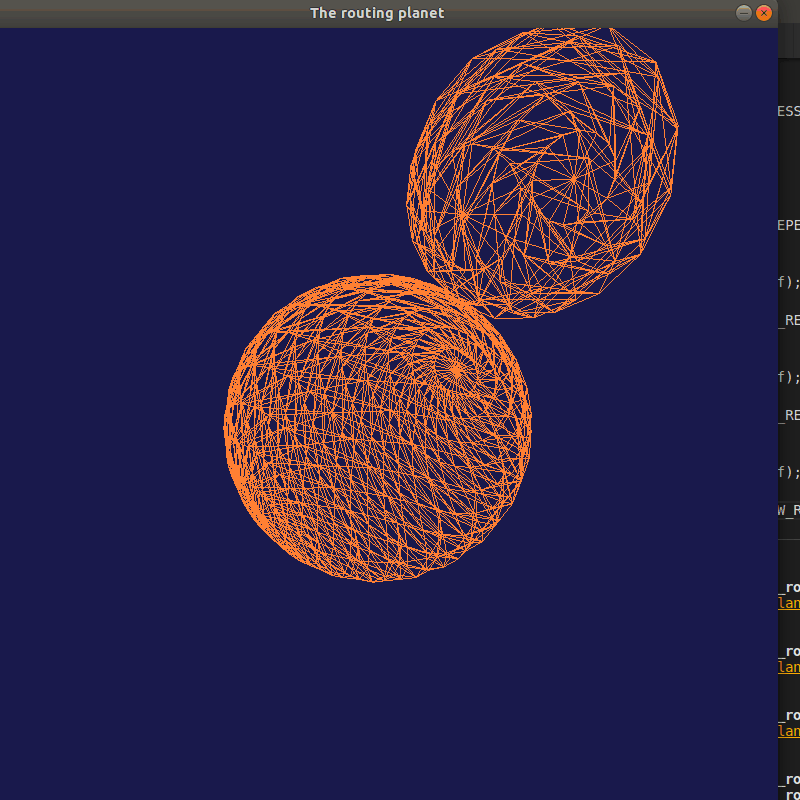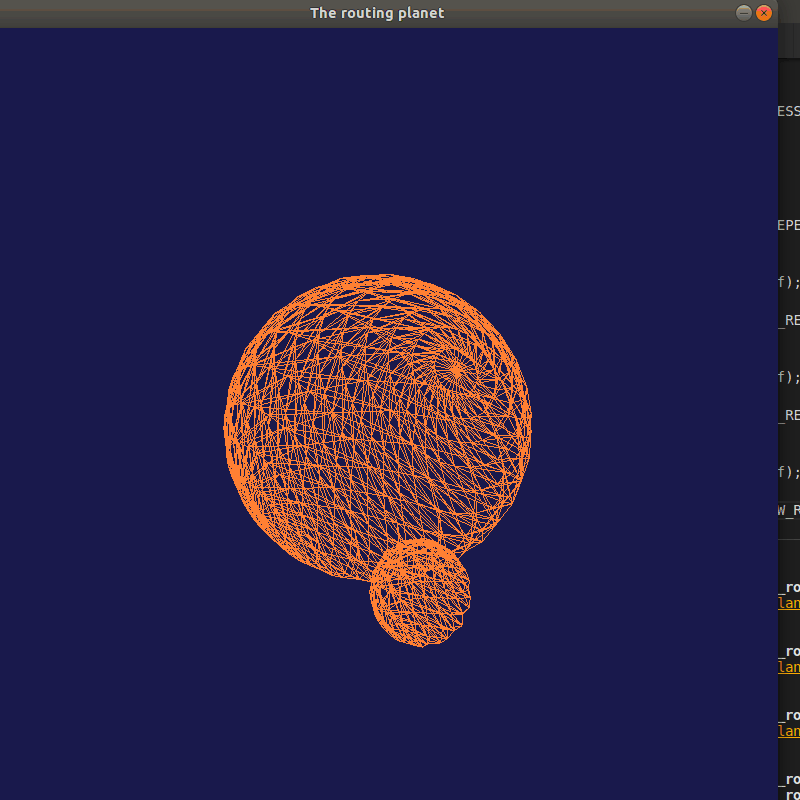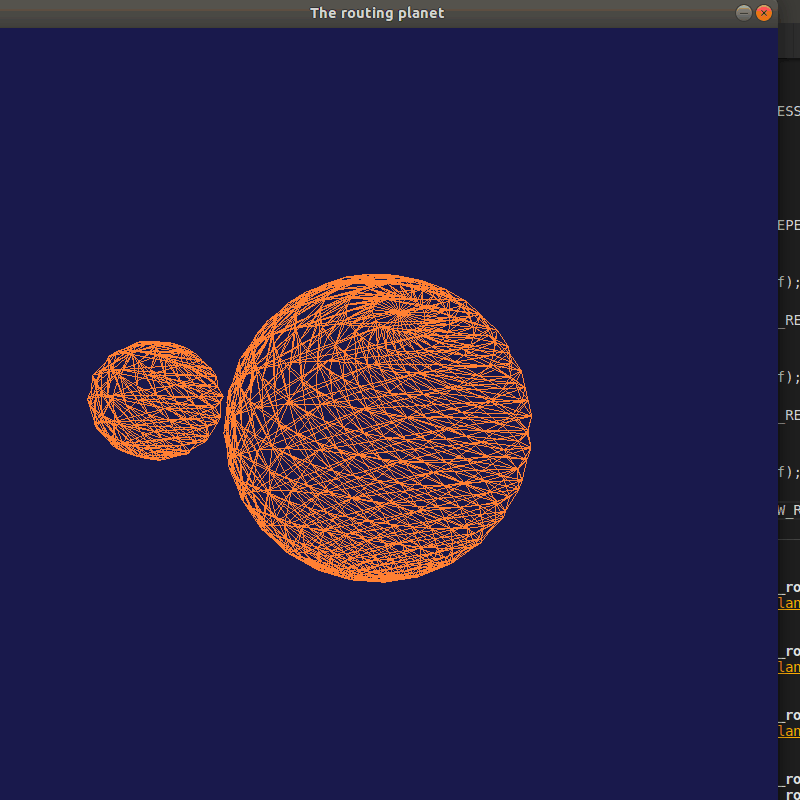
星球公转与自转

  • 更新：将公转矩阵与摄像机矩阵分离，公用变换（摄像机、透视）与各个物体的单独变换分离，使代码更符合逻辑。

环境说明

  • 开发环境：Linux
  • 运行环境：Linux
  • 运行方式：
    • 打开终端，用export LD_LIBRARY_PATH=./../dll，增加动态库搜索路径
    • 运行可执行文件./planet_rotation
    • 若失败，则按照GLFW、GLEW的配置方法配置好环境后在本机重新编译
    • 附有运行成功的demo，可以作为参考
  • 使用库：GLFW、GLEW、GLM

运行结果

  • ESC：退出程序
  • D：按下后逆时针自转
  • shift+D：顺时针自转
  • Y：按下后逆时针公转
  • shift+Y：顺时针公转
  • 方向键：旋转观察视角

  • 公转与自转：
    不交互

  • 改变旋转方向：
    控制自转公转方向

  • 更改观察视角
    控制观察视角

    实现过程

  1. 生成球体：

    • 生成顶点：遍历每个纬度、经度，计算纬度、经度映射到球体上的坐标
    • 生成球面三角：在北极点与南极点处，与相邻纬度生成三角；在其余纬度上，与相邻纬度生成四边形（即两个三角）

  2. 生成缓冲区：将生成的球体顶点与顶点索引绑定至缓冲区，VAO分别为SUM和PLANET，代表大球（太阳）及小球（行星）

  3. 生成着色器
  4. 绘制：View作为摄像机视角，Projection为透视矩阵，这二者为全局公用。
    1. 按处理对象，分为两种矩阵——公共矩阵及单个模型的矩阵；
    2. self_trans设为小球的旋转矩阵，管理自转；
    3. position_trans设为小球的轨道初始坐标
    4. public_trans设为小球的坐标矩阵，管理公转；
    5. 按照mvp = Projection * View * public_trans * position_trans * self_trans;顺序管理小球——先自转，再移动，后以透视视角形变。
    6. 分别绑定两个缓冲区，分别绘制两个星球。
  5. 交互：设置键盘事件，管理自转与公转的旋转角度
    • ESC：退出程序
    • D：按下后逆时针自转
    • shift+D：顺时针自转
    • Y：按下后逆时针公转
    • shift+Y：顺时针公转
    • 方向键：旋转观察视角

知识点

  1. 多个物体绘制:

    当多个物体需要绘制时，每个物体有自己的顶点缓冲区、顶点索引缓冲区，因此为每一个物体设置一个顶点数组（VAO），此后每次需要此物体时，直接绑定该顶点数组，同时绑定内部的数据格式。

  2. 球体生成：

    遍历球体的每个纬度、经度，通过三角函数运算得到对应经纬度的正交右手系坐标:

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    for (unsigned int i=0; i <= HorSlide; i++){
        float hor_angle = hor_step * i;
        float z_cur = radius * cos(hor_angle);   //z原点坐标
        float r_cur = radius * sin(hor_angle);   //纬度平面半径

        for (unsigned int j=0; j <= VerSlide; j++){
            float ver_angle = j*ver_step;
            float x_cur = r_cur * cos(ver_angle);   
            //顶点入vector 
            vects.push_back(x_cur+x);
            vects.push_back(y_cur+y);
            vects.push_back(z_cur+z);
    ... ...

    并对每个相邻的纬度生成球面三角:

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    //插入球面三角形顶点索引
    if (i > 0 && j > 0){
        //若以自我为一个四边形的右下角，其绘制曲面三角的点：
        unsigned int ru = index - VerSlide;
        unsigned int lu = index - VerSlide - 1;
        unsigned int ld = index -1;
        unsigned int rd = index;
        //上或下一圈为一个点，添加的为三角形
        if (i == 1){               
            inds.push_back(ru);
            inds.push_back(ld);
            inds.push_back(rd);
        }
        else if (i == HorSlide){
            inds.push_back(ru);
            inds.push_back(lu);
            inds.push_back(rd);
        }
        //四边行情况——添加两个三角形
        else{
            inds.push_back(ru);
            inds.push_back(ld);
            inds.push_back(rd);
            inds.push_back(ru);
            inds.push_back(lu);
            inds.push_back(ld);
        }
    }

  3. 旋转变换：

    • 公转：通过旋转摄像机函数，得到公转的效果，同时反向等速旋转大球，使其独立于公转不旋转：

      1
      2
      View = glm::rotate(View, glm::radians(public_rotate), glm::vec3(0, 0, 1.0f));   //旋转视角以公转
      model = glm::rotate(model, glm::radians(-public_rotate), glm::vec3(0, 0, 1.0f)); //旋转大球以让大球看起来静止

    • 自转：在绘制完大球后，绑定小球缓冲区，并计算自传的变换矩阵。其中，最关键的是 绕任意轴旋转:

      1. 将小球移动至原点
      2. 在原点对小球进行旋转
      3. 将小球移动回自己的轨迹
      4. 生成变换矩阵，绘制。
        1
        2
        3
        4
        5
        6
        7
        8
        9
        10
        11
        12
        13
        14
        15
        16
        17
        18
        glBindVertexArray(PLANET);
        planet_self = planet_self + self_rotate;
        if (planet_self > 360)
            planet_self -= 360;
        else if (planet_self < 0)
            planet_self += 360;
        planet_public = (planet_public + public_rotate);
        if (planet_public > 360)
            planet_public -= 360;
        else if (planet_public < 0)
            planet_public += 360;
        glm::mat4 public_trans = glm::rotate(model, glm::radians(planet_public), glm::vec3(0, 0, 1));
        glm::mat4 position_trans = glm::translate(model, position);
        glm::mat4 self_trans = glm::rotate(model, glm::radians(planet_self), glm::vec3(0, 0, 1));
        mvp = Projection * View * public_trans * position_trans * self_trans;
        glUniformMatrix4fv(transformLoc, 1, GL_FALSE, glm::value_ptr(mvp));

        glDrawElements(GL_LINE_STRIP, indsP.size(), GL_UNSIGNED_INT, (void*)0); // we use index buffer, so set it to null.

  4. 按键交互：转自

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    key include/GLFW/glfw3.h 中定义的 GLFW_KEY_* 包含一些按键的ASCII码
    scancde
    action 按键动作
    GLFW_RELEASE 松开
    GLFW_PRESS 按下
    GLFW_REPEAT 重复，一直按着
    mods 按键模式
    GLFW_MOD_SHIFT 按下Shift键
    GLFW_MOD_CONTROL 按下Ctrl键
    GLFW_MOD_ALT 按下Alt键
    GLFW_MOD_SUPER

实验过程

  1. 最后一个顶点总在原点——总有个“小尾巴”与原点相连
    0,0,0 with tail
    1,1,0 with tail
    index算错，整体向后偏移一个，因此最后一个index对应的点在原点，更改后：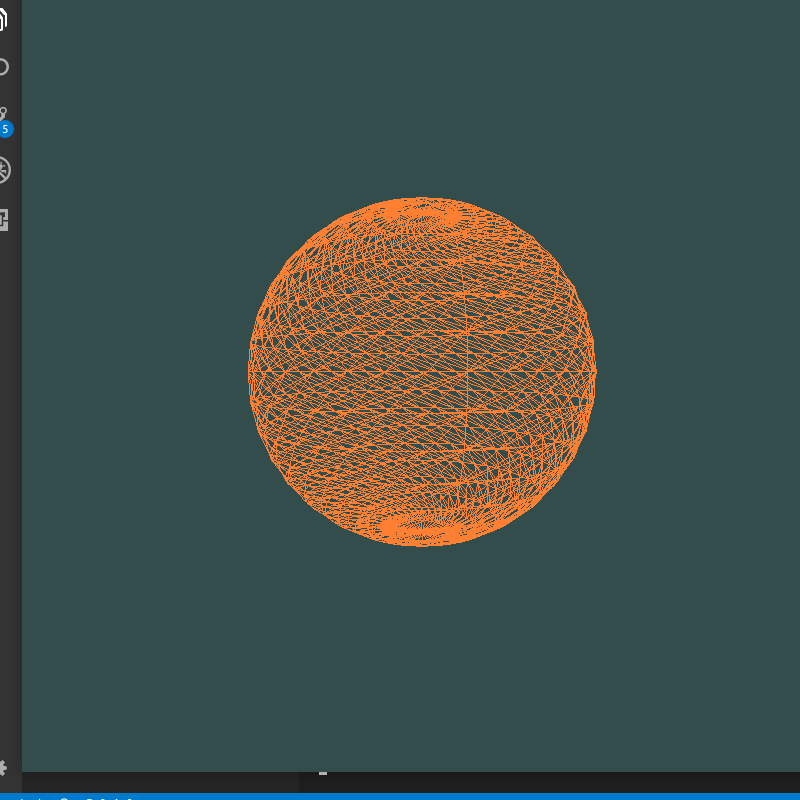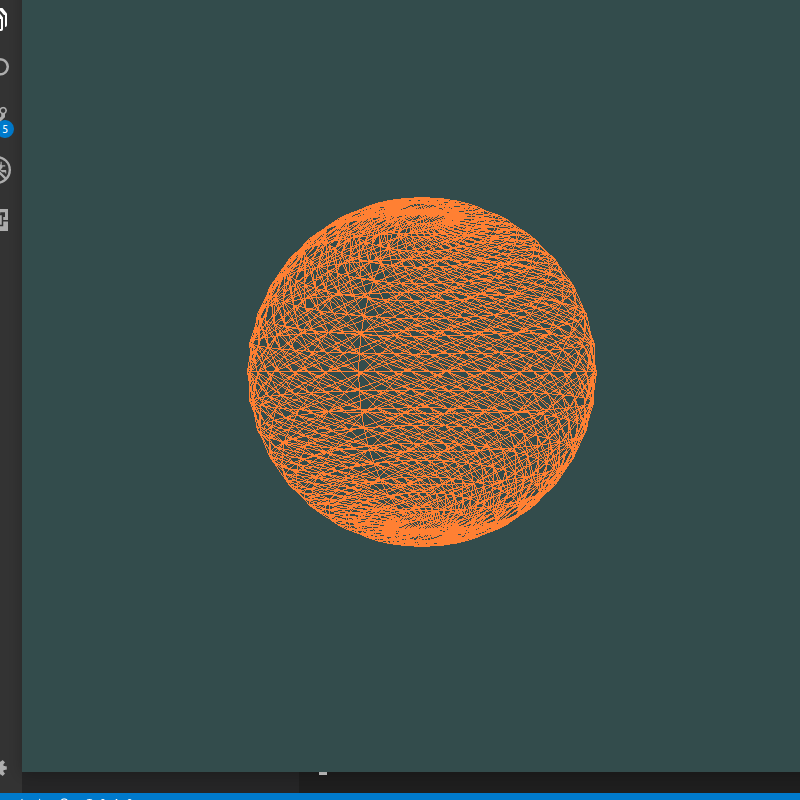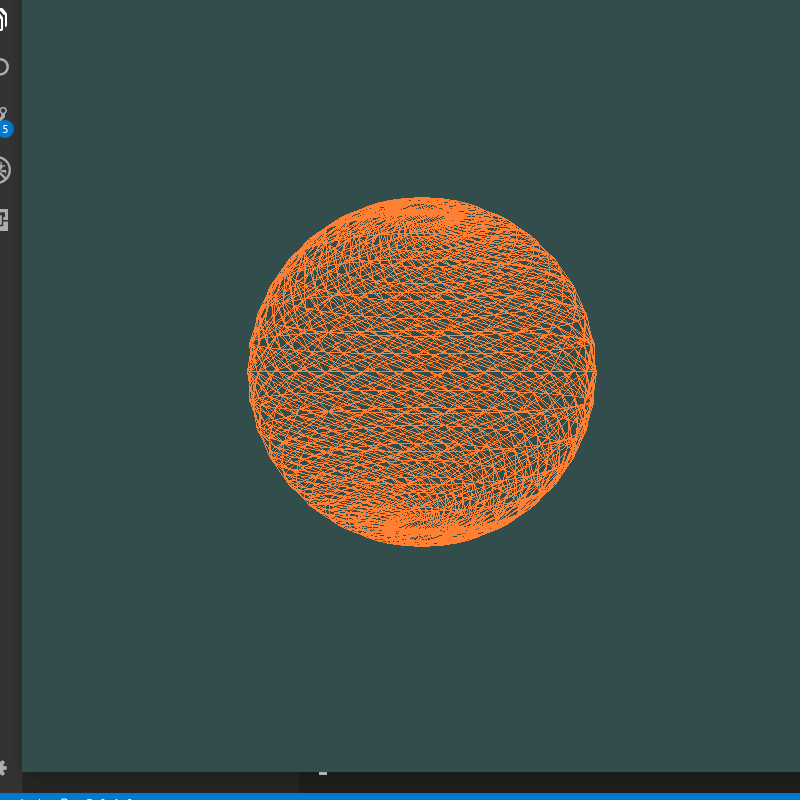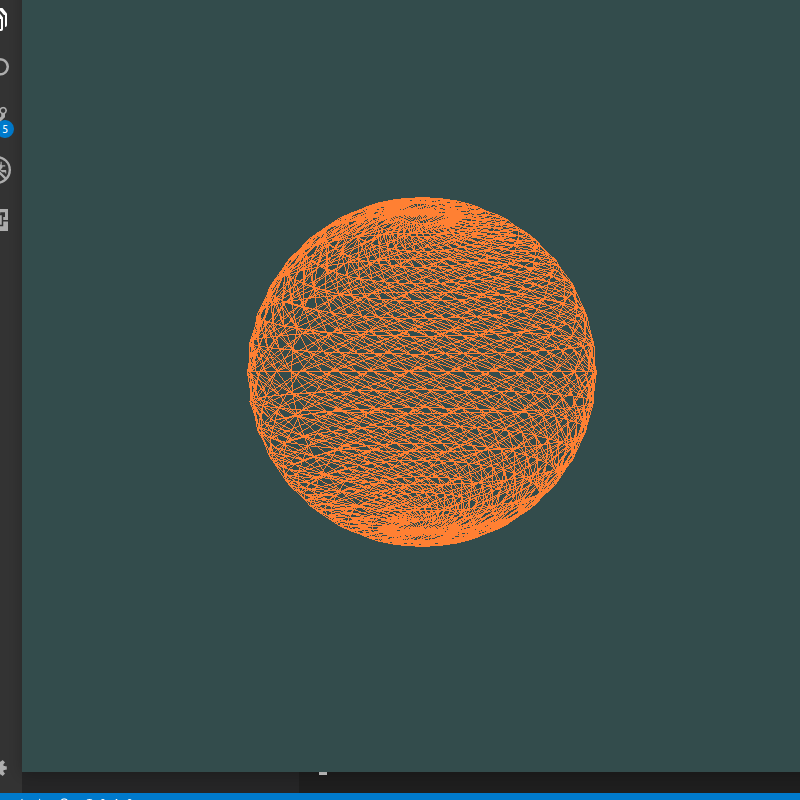
    0,0,0 without tail
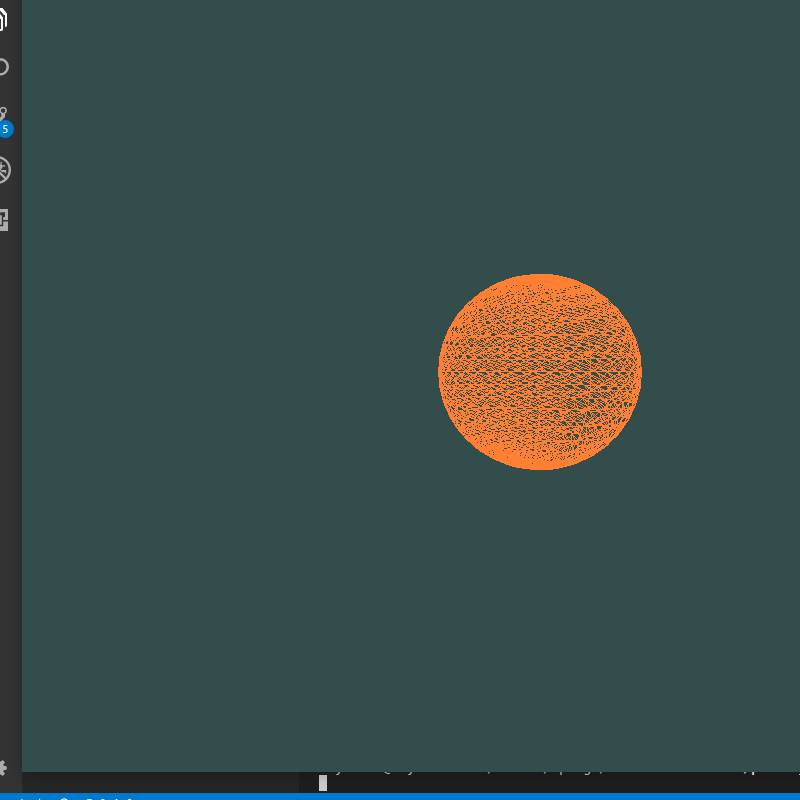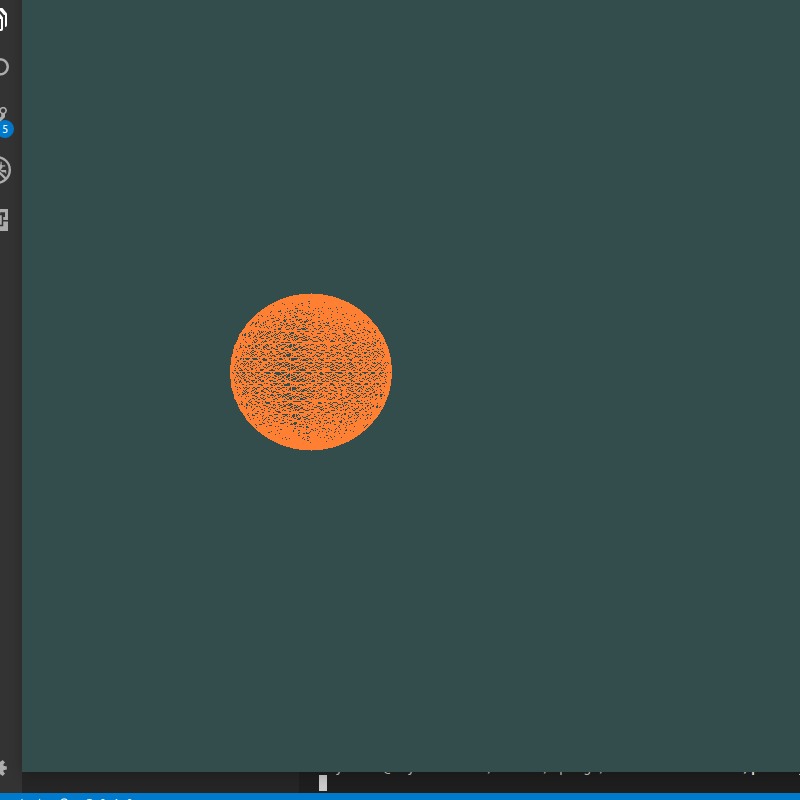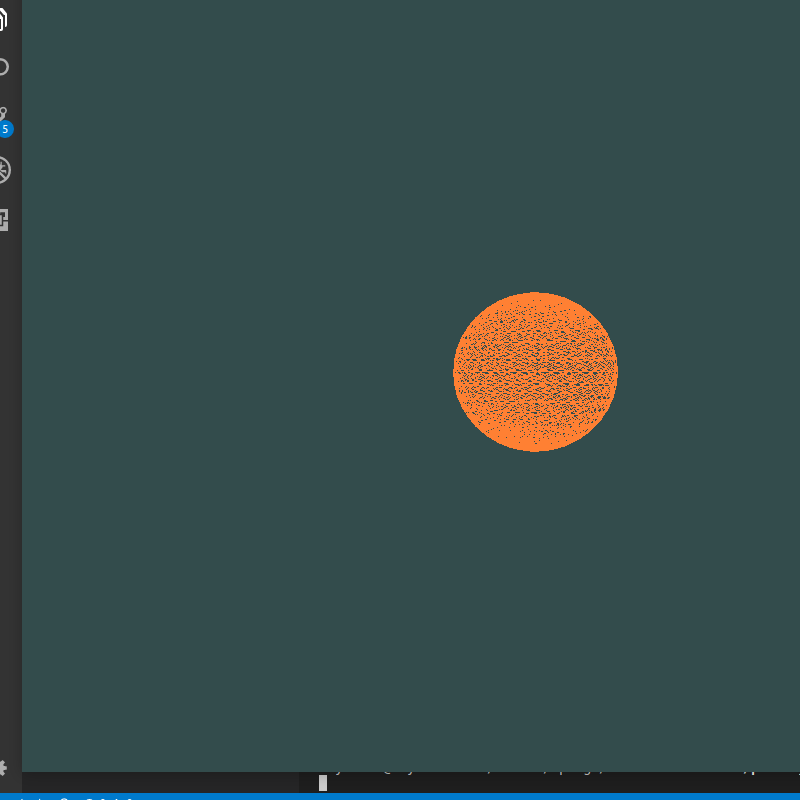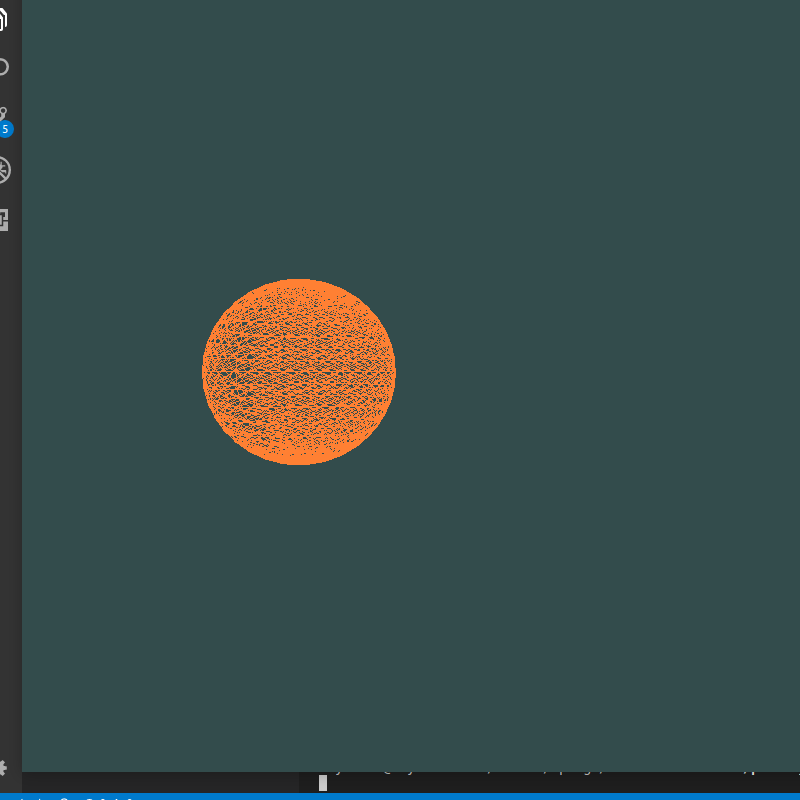
    1,1,0 without tail

  2. 生成圆时ｚ坐标偏移出错:
    0,0,1 with tail -- broken
    输出坐标发现，z的坐标在不断叠加：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    -8.74228e-08 0 0
    -8.63465e-08 -1.36759e-08 1
    -8.3144e-08 -2.70151e-08 2
    -7.78943e-08 -3.96891e-08 3
    -7.07265e-08 -5.13858e-08 4
    -6.18172e-08 -6.18172e-08 5
    -5.13858e-08 -7.07265e-08 6
    -3.96891e-08 -7.78943e-08 7
    -2.70151e-08 -8.3144e-08 8
    -1.36759e-08 -8.63465e-08 9

原来是z坐标没有在纬度平面上循环时重置……

1
2
3
4
5
6
7
8
//根据原点坐标，进行平移
x_cur += x;
y_cur += y;
z_cur += z;
//顶点入vector 
vects.push_back(x_cur);
vects.push_back(y_cur);
vects.push_back(z_cur);

改为以下即可：

1
2
3
vects.push_back(x_cur+x);
vects.push_back(y_cur+y);
vects.push_back(z_cur+z);

0,0,1 success

源代码

参考资料

球体生成

按键